| 中沢: |
「RC造壁の復元力特性はどのような履歴をしめしますか?」 |
| 島課長: |
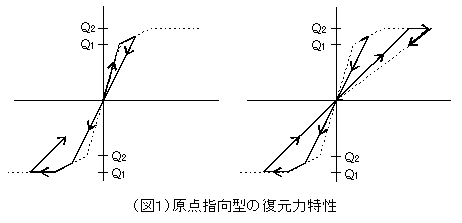
「原点指向型の復元力特性(図1)をせん断変形の特性として使用するね。」
|
| 中沢: |
「この復元力特性の特徴はどのへんにあるのですか?」 |
| 島課長: |
「除荷時の剛性が原点へ戻る勾配をもつため、変形量が大きいほど剛性低下が著しく、また最大変形よりも小さい繰り返しでは、履歴ループを描かず、直線的変化するため、履歴減衰がまったく得られないせん断挙動の特色をもっているんだ。」 |
| 中沢: |
「なるほど!せん断変形する要素に用いるわけですね。」 |
| 島課長: |
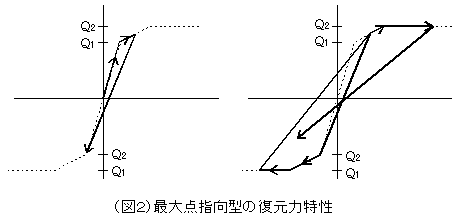
「同じせん断変形でも、短柱やスパンの短い梁のように、曲げ変形も含みながらせん断変形も大きい場合には、最大点指向型の復元力特性(図2)を用いたりするね。」
 |
| 中沢: |
「いろいろあって、なかなか簡単に話しがすまないですね。」 |
| 島課長: |
「その通りだね。ここで話していることも表面的なことで、もっと奥の深い話しはたくさんあるはずなので、謙虚に勉強したり、いろいろな人に聞いてみることだね。」 |
| 中沢: |
「はい!わかりました。もう少し教えて欲しいのですが、さらに復元力特性はありますよね。」 |
| 島課長: |
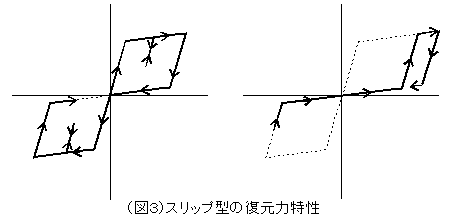
「とにかくたくさんあるね。例えばブレースなどに使用するスリップ型の復元力特性(図3)は次のようになるね。」
|
| 中沢: |
「ブレースとしてまだピンとこないのですが、この図は引張り時のブレースと圧縮時のブレースが対称形の同様な挙動になるんですか?」 |
| 島課長: |
「そうではないんだ。この復元力特性はラーメン構造に組み込まれたX配置のブレースで、引張側ブレースのみ働き、圧縮力は負担しないと考えたときの特性だね。」 |
| 中沢: |
「と言うことは、圧縮力が負担できないわけですから、座屈しやすい細いブレースの場合と考えて良いわけですね。」 |
| 島課長: |
「そうだね。H型鋼ブレースのように圧縮力も充分負担できるようなものは、標準型(第29話の図1)の復元力特性を用いたりするね。」 |
| 中沢: |
「はい、わかりました。最近、急激に普及している積層ゴムはどのような特性をもちますか?」 |
| 島課長: |
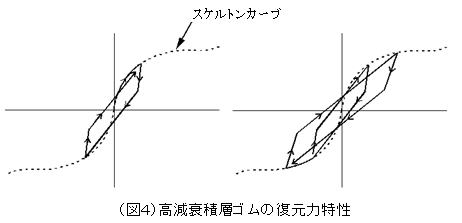
「オイレス工業の鉛入り積層ゴムやブリヂストンの高減衰積層ゴム等メーカーによりその復元力特性は異なるね。例えば高減衰積層ゴムの復元力特性(図4)は次のようになる。」
|
| 中沢: |
「かなり複雑な挙動をしますね。」 |
| 島課長: |
「そうかな?これらの履歴ループについて説明してみよう。スケルトンカーブと言う骨格曲線(図4点線)があるね。まずはこの線上を動く、除荷が起こるとバイリニアのループを描くようになるんだ。それゆえ、歪依存型の修正バイリニアモデルとも呼ばれるね。」 |
| 中沢: |
「まだ良くわからないのですが、この図で除荷が起こった後、小振幅のループと、逆に大振幅のループがあるように感じますがどのような変化がありますか?」 |
| 島課長: |
「そうだね。除荷後の小振幅では、バイリニアモデルと同様に第1又は第2剛性を持ちながら履歴ループを描くんだ。一方、変形がそれまでに経験した最大値を上回る場合には、スケルトンカーブ上を進み、そしてまた除荷が起こるとバイリニアの履歴ループになる。これらの挙動を繰り返すことになるね。」 |
| 中沢: |
「この図から考えると、変形が大きくなるにつれて、除荷時の剛性は小さくなっていますね。」 |
| 島課長: |
「そうともいえないね。変形が大きくなると、スケルトンカーブ(図4点線)が立ち上がるところで除荷剛性が大きくなるところがあるね。これらの積層ゴムを使った免震層の挙動について、応答履歴ループ(図5)を描いた例は、次のようになるね。」
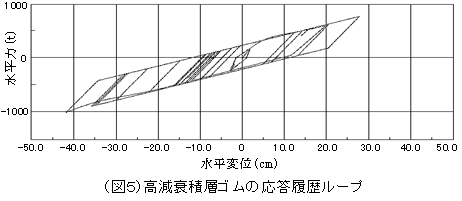
|
| 中沢: |
「スケルトンカーブ上を進んでいるのがよくわかりますね。」 |
| 島課長: |
「BUILD.DD2000(弾塑性地震応答解析プログラム)においては、この履歴ループを時々刻々とディスプレイ上で見ることができるんだ。もちろん、時刻を止めて途中までの結果を確認したり、また続行させたりもできるね。」 |
| 中沢: |
「それは便利ですね。やはり初めての経験なのでそれらの挙動を目で確かめることは、理解しやすいですよね。」 |
| 島課長: |
「さて、部材の復元力特性は、更にたくさんあることは先程述べた通りだが、後は、中沢君の研究に任せるとして、最後にR.Oモデルについて話してみよう。」 |
| 中沢: |
「なんですか、R.Oモデルとは?」 |
| 島課長: |
「Ramberg-Osgoodモデルと言う復元力特性 (図6)で次のような履歴を描くね。」
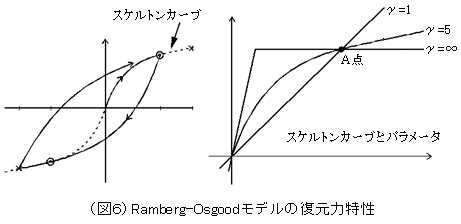
|
| 中沢: |
「これは、スケルトンカーブだけでなく、除荷時の履歴ループもなめらかな曲線となっていますね。」 |
| 島課長: |
「そうだね。この復元力特性の特徴は、スケルトンカーブを作り出すA点やγのパラメータを変えるだけで、スケルトンカーブが様々な曲線に変化するだけでなく、弾性時剛性のような直線式や完全弾塑性型まで表すことができるんだ。」 |
| 中沢: |
「と言うことは、うまくパラメータを変化させてスケルトンカーブをあわせることが出来れば応用は多いですね。」 |
| 島課長: |
「そう言うことだね。しかし今まで話したようにスケルトンカーブだけの一致ではすまず、除荷時の剛性や履歴ループから導き出される等価粘性減衰定数等も合わせて一致させる必要はあるよね。」 |
| 中沢: |
「よくわかりました。この特性は、一般にどのようなものに使われますか。」 |
| 島課長: |
「鉄筋コンクリートの曲げによる復元力特性や、土のせん断による復元力特性にはよく使われるし、また、免震層の復元力に使われることもあるね。」 |
| 中沢: |
「これでよくわかってきました。後は、構造部材の特性を把握して、いかにこれらの復元力特性をあてはめられるかという応用ですね。」 |
| 島課長: |
「そのとおりだね。次は串ダンゴにモデル化したときの、層レベルの復元力特性をどう取り扱うかだ・・・。」 |
|
(星 睦廣) |













