| 中沢: |
「周期の異なるsin波を重ね合わせると複雑な波が得られ、逆にたどると複雑
な波や挙動はいくつかの基本パターンへ分解されるということですね。
sin波などがでてきたのでアカデミックな話になってきたなと思ってかまえ
てしまいましたよ。」 |
| 島課長: |
「数式等は教えてもらって理解できるものでもなく、やはり自分自身でじっくり考え修得するものだね。だから、そのような理論的なことはともかく、感覚的
なところで少しでも伝わるような話し方ができればな、と思っているんだ。」 |
| 中沢: |
「島課長、いつもありがとうございます。わかりやすいヒントは、本当に助かります。話を頂いた後は、いつも明かりがパッとついたような気がするんですよ。」 |
| 島課長: |
「おいおい、そんなにほめなくていいよ。話をもとに戻そうか。」 |
| 中沢: |
「はい、その・・・基本パターンという言葉がでてきましたが、これと建物の固有周期とどうつながってくるんですか。」 |
| 島課長: |
「結論を先に言うと、基本パターンが固有ベクトルでその周期が固有周期だ。」 |
| 中沢: |
「一気に話されたので、まだ理解するに至っていません。固有ベクトルという新
しい言葉が出てきましたが?」 |
| 島課長: |
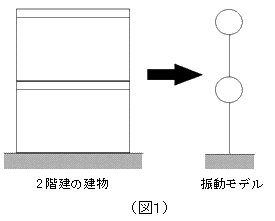
「固有ベクトルとは、建物のもつ固有な振動形のことなんだが、この固有な振動 形とは、物理的にどのようなことかについて説明しよう。 2階建の建物を串ダンゴ型の振動モデルにおきかえてみる。このとき、床レベ
ルにその層の重量を集め一つのダンゴにし、柱の剛性を一本の串でモデル化すると、質点系の振動モデルができるね。」
|
| 中沢: |
「この串ダンゴモデルはよく見るんで感覚的には分かりますね。ただ、複数本あ
る柱を一本の串状の柱にモデル化するわけですね。この辺を具体的にどうやるかは、まだわかりませんが。」 |
| 島課長: |
「その点については、後で教えるとして、まずこのモデルにおける建物固有の振動形とは何か?だ。」
|
| 中沢: |
「固有というからには、その建物だけがもつ特性ですね。」
|
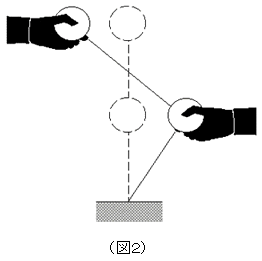
| 島課長: |
「もちろんそうだ。このような串ダンゴの模型を作ったとして次のような実験をしてみる。まずダンゴの部分を両手で持ち、左右に少し水平変位をさせるんだ。その後パッとはなす。」
|
| 中沢: |
「すると、当然振動を始めますね。かなり複雑な振動ですね。」
|
| 島課長: |
「そうなんだ、このようにして振動させると複雑な振動をするんだが、初期水平変位において、一質点目の変位と二質点目の変位がある値になったときに限って正常な振動をするんだ。」 |
| 中沢: |
「正常な振動とは、どういうことですか?」 |
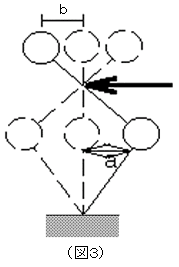
| 島課長: |
「図3において矢印の点がまったく移動しないで、左右対象のきれいな振動をするんだ。」
  |
| 中沢: |
「左右対象の振動をするということは、なにを意味するんですか?」 |
| 島課長: |
「左右対象に振動しているということは、まず第一に、一質点目の水平変位と二質点目の水平変位の比がいつの時刻をとっても一定であるといえるね。第二に、どの質点も同じ周期で動いているということだ。すなわち、二質点目の水
平変位をY軸にとり、時刻をX軸にとると、cosカーブを描くのがわかるね。一質点目も同様に描けて、どちらもそのカーブの周期は同じということだ。」 |
| 中沢: |
「なるほど、各質点の水平変位の比が一定で、どの質点も周期が同じという特別な状態のときを示しているんですね。」 |
| 島課長: |
「そうなんだ。この特別な状態のときの周期を固有周期と呼び、水平位の比(無次元量)を固有ベクトル又は固有振動形というんだ。」 |
| 中沢: |
「このような特別な状態になるときは、この振動形以外には起こらないんですか?」 |
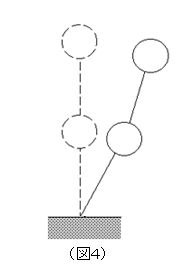
| 島課長: |
「もう一つあるんだ。図4のように同一方向に変形させて離すことにより、定常な振動を始める状態のときだ。」 |
| 中沢: |
「なるほど、この状態のときを一次の固有周期と呼び、さきほどの状態を二次の固有周期と呼んでいるんですね。」
|
| 島課長: |
「そうなんだ、今、二質点のモデルだから二次までしかないが、三質点であれば、一次、二次、三次の3つの固有値が存在するんだ。どのような振動形かは後で調べてみるといいね・・・。」 |
| 中沢: |
「島課長!固有値についてはよくわかりましたが、まだはっきりしないところが
あります。というのは、建物がもつ特別な振動状態のときをその建物の固有値
と呼んだとしても、通常の場合は、各質点はとても複雑な挙動を示すと思うんですよね。すなわち、この複雑な挙動と、固有値といわれた定常な振動との関係がどうなのか?という点ですが。」 |
| 島課長: |
「大事なことはそこなんだよ。複雑な振動とどんな関係があるかだ。それは冒頭で話したところとつながってくるんだ。」 |
| 中沢: |
「え〜と。複雑な挙動もいくつかの基本パターンへと分解されるということです
か?」 |
| 島課長: |
「そこなんだ、そのことを具体的に話してみると・・・。先ほどと同様に、任意の初期水平変位を与えてパッと開放すると、かなり複雑 な挙動を、各質点は示すはずだ。しかし、この複雑な挙動も基本パターンの集合として考えられ、その基本パターンが一次の周期をもつ波動形であり、同様に二次、三次であるということなんだ。」 |
| 中沢: |
「少しわかりかけてきましたが、整理すると、建物は自分自身がもつ固有の各次の振動形を重ね合わせた挙動をしても、固有値とは関係のない成分の動きはないということですね。」 |
| 島課長: |
「そのとうりだ・・・。ただここで注意してほしいのは、地震波のような波が入力された場合には、建物のもつ固有値とは関係ない成分も入ってきて、さらに複
な挙動をしめすことになるんだ。」 |
| 中沢: |
「ということは、純粋に建物の固有値だけで挙動するときとは、どんな条件のと
きですか?」 |
| 島課長: |
「それは強制的に任意の初期変位を与え、パッと解除して、そのあとは自由振動 させたときだ。または各質点に瞬間的に外力を加え、その後は自由振動をさせたときだね。」 |
| 中沢: |
「なるほど、建物に自由振動をさせたときには、建物自身がもつ固有値成分のみが重ね合わさったときの挙動をするということですね。」 |
|
(星 睦廣) |













