（株）構造ソフト　地震動応答解析のおはなし　第１０話「振動解析の目的は？（その１）」

■地震動応答解析のおはなし

トップページ > 技術情報 > 地震動応答解析のおはなし > 第１０話

第１０話　「振動解析の目的は？（その１）」

中沢：

「あらためてお聞きしますが、なぜ振動解析をするんですか？」

島課長：

「振動解析する目的は何か？ということだね。」

中沢：

「そうです。通常の建物は振動解析をやりませんが、高層建物等は振動解析するように義務づけられていますね。何を知るために振動解析をするのでしょうか？」
「わかりやすく一言でいうならどういう言葉になるのですか？」

島課長：

「何を知るために振動解析をするのか？との疑問に的確に一言で答えるのは難しいが、あえて一言で言うなら、建物に作用する地震力の大きさを知るために行うと言うことかな。」

中沢：

「建物に作用する地震力の大きさを知るためですか？意外でしたね。」

島課長：

「どうして意外なんだね。」

中沢：

「振動解析は私たちにとっては高尚な解析ですから、もっと難しいレベルの話があるのかと思ったんですよ。」

島課長：

「ふむ、ふむ・・・。」

中沢：

「そこで、私なりに振動解析をやる目的は何か？と考えてみたのですが・・・。すなわち、柱梁で構成した立体の骨組モデルがある。これに地震波を入力して地震動応答解析をする。この結果として得られた各部材の最大応力に対して、許容応力度設計をしてやる、と言うふうにです・・・。」

島課長：

「まあ、いいんじゃない。そのとおりだね！」

中沢：

「課長！本当ですか？」

島課長：

「いや、中沢君の言うことの方が的を得た答えかもしれないね。」

中沢：

「え！正しいんですか？」

島課長：

「正しいね。しかし我々が振動解析するときに、柱梁で構成した立体の骨組モデルを用いて解析するのではなく、建物を串ダンゴにモデル化したもので行うんだ。」

中沢：

「そうそう、そこなんですよ。わからないのは。串ダンゴのモデルが出て来たとたんに、振動解析する目的はどの辺にあるんだろうと悩んでしまうんですよ。」

島課長：

「なるほど、なるほど。」

中沢：

「ところで、まだわかったような感じがしません。いやむしろ、ぜんぜんわかってないんですが・・・。」

島課長：

「それではもう少し話をすすめよう。建物を等価な串ダンゴにモデル化できたと仮定しよう。その串ダンゴモデルに、ある地震波を入力して応答解析をすると、各層の最大せん断力（図２のQ）が得られる。」

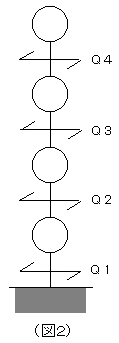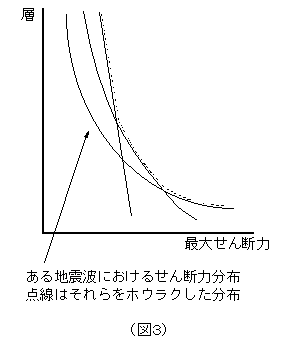
「同様にして、別な地震波を入力すると、各層の最大せん断力は、先程とは異なる分布を示すはずだ。」
「さらに同じことを繰り返して最大せん断力分布を描き、そしてそれらを包絡クしたせん断力分布が得られる。（図３・点線で示した分布）」

中沢：

「このせん断力分布が、先程言っていた振動解析の目的である建物に作用する地震力の大きさを表しているわけですね。」

島課長：

「そういうことだ。」

中沢：

「しかし、このせん断力分布をどう使うんですか？」

島課長：

「これを外力として一次設計を行うんだよ。」

中沢：

「え！静的解析をするんですか？」

島課長：

「そのとおり。中沢君が先程話したように許容応力度設計を従来通りの方法で行うってわけだ。」

中沢：

「あれ、ちょっと待って下さい。あまりにも単純な話なのでかえってとまどってしまいましたが・・・。」

島課長：

「さて、少し整理しないといけないね。まず、今までの話しは、弾性範囲内である一次設計的な考え方での振動解析について論じているということだ。」
「別な言い方をすると、レベル１の地震動に対して、どれだけの地震力（せん断力）が建物に作用するかを、振動解析を通して見つけ出そうとしていたわけだ。振動解析の目的として〔建物に作用する地震力の大きさを知る〕とは、あくまでもレベル１のときであり、レベル２や免震における目的は異なってくるということを頭の中に入れておいてほしいね。」

中沢：

「わかりました。それらについての目的は、また後で教えて下さい。まずは先程の話しで〔建物を等価な串ダンゴにモデル化する〕と述べておりましたが、どのくらい近似したモデル化となるんですか？」

島課長：

「弾性範囲内の解析のときは、近似したモデル化でなく、完全に等価なモデル化と言えるんだ。」

中沢：

「完全に等価なモデル化とは・・・？」

島課長：

「柱・梁で構成した立体モデルをそのまま振動解析した場合と、串ダンゴにモデル化して解析した場合と、どちらも計算結果は同じだということだ。」

中沢：

「え！なぜ簡略化したモデルなのに同じ結果を導き出すのですか？」

島課長：

「簡略化したモデルという表現は正しくないね。正確に言うなら、〔階の自由度に縮合した弾性剛性マトリックスにおける曲げせん断型の串ダンゴモデル〕と呼んでいるね。」

中沢：

「島課長！チンプンカンプンです。」

島課長：

「応力解析するときは、変位法を用いていることは知っているよね。」

中沢：

「変位を未知数とするもので、p＝kxのつりあい式で表されたりする話しですよね。」

島課長：

「そう、pは外力、kは剛性、xは変形だ。｛p｝＝［k］｛x｝このように表すと｛p｝は外力ベクトル、［k］は剛性マトリックス、｛x｝は変形ベクトルと呼ぶね。」

中沢：

「ベクトルやマトリックスの話しになると、少し弱いですね。」

島課長：

「中沢君が中学生のときに、3元連立方程式というのを習ったはずだが・・・。」

中沢：

「ええ・・・。未知数が3つあって、式が3つある。」　　　　

	x＋y＋z＝6
	2x＋y－z＝1	（イ）式
	x＋2y－2z＝-1

「これのx，y，zを求めよ、というやつですね。」

島課長：

「そうそう、そのような式だよ。それを解くときにまずやることは、xを消去してyとzだけの式にするよね。先程の例では、

	-y＋3z＝7
	y＋3z＝11	（ロ）式

となる。マトリックスで表示すると

	-1	3	y7
	1	3	z11

となる。ここで大事なことは、マトリックスの大きさが、3×3から2×2のマトリックスに縮合されたが、(イ)の式のy，zの値と(ロ)の式のy，zの値は同じだということだ。」

中沢：

「島課長！何を言いたいか、まだ理解できていないのですが。」

島課長：

「柱・梁で構成された立体の建物モデルがある。そこには未知数となる変形が何百とあり、これを解くために、何百元の連立方程式ができあがる。ここで未知数を一つずつ消去して、各階の自由度(変形)だけが残るまで消去を続ける。そこで得られたマトリックスが、縮合した弾性剛性マトリックスというんだ。それをモデルで表すと、曲げせん断型の串ダンゴモデルとなるわけだ。」

中沢：

「なるほど・・・。このモデルで振動解析した各層の変形は、立体モデルで解析したのと同じ変形が得られるわけですね。」

島課長：

「そのとおり、弾性時における振動解析の目的が、建物に作用するせん断力を知ることからすると、それを知るための最も縮合化されたモデルが各層の自由度だけ残した串ダンゴモデルということになるわけだ。」

中沢：

「大変よくわかりました。」

（星睦廣）

[第９話へ]　[１０話]　[第１１話へ]

[地震動応答解析のおはなしへ戻る]