| 中沢: |
「振動解析は剛性が命、とてもよく解りました。弾性剛性においても、いろいろ奥の深い話しがあるものだと感心しています。」
|
| 島課長: |
「剛性評価がいかに重要であるか、わかったと思うね。」
|
| 中沢: |
「ところで、振動解析の話しは、弾性の挙動の範囲に留まらず、当然弾塑性の範囲まで剛性評価をしなければならないと思いますが、弾塑性剛性の扱いはどうなるのですか。」
|
| 島課長: |
「当然、剛性は厳密に評価しなければいけないという点では、弾性のときも弾塑性のときも同じだね。」
|
| 中沢: |
「そこで、まだよく解らないのは、弾性の場合は、リダクションという数学的な処理が入って、串ダンゴ系にモデル化できましたが、弾塑性剛性の場合にはどの様な手順でそれを導きだすのか、その辺を教えて下さい。」
|
| 島課長: |
「まず、弾塑性剛性について話すならば、柱材や梁材の部材レベルの剛性から話した方がわかり易いね。」
|
| 中沢: |
「部材レベルで言うなら、弾性状態の剛性と完全に寝てしまう塑性化後の剛性とありますね。」
|
| 島課長: |
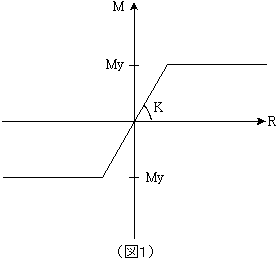
「そう、S造であるなら曲げが正負対称のバイ・リニア型(図1)の剛性になるね。そして、Myは全塑性モーメントにとるのが一般的だ。」
|
| 中沢: |
「RC造柱は?」 |
| 島課長: |
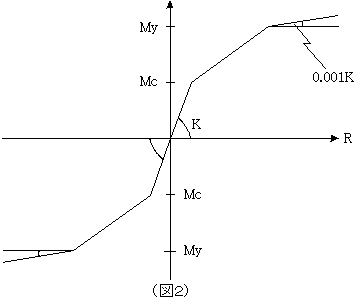
「図2のように、ひび割れが起こるから、ひび割れモーメント(Mc)のところから第2勾配となり終局モーメント(My)後が第3勾配となるね。」
|
| 中沢: |
「この第2勾配と第3勾配はどのくらいの勾配ですか?」
|
| 島課長: |
「まず、簡単な第3勾配から話すと弾性剛性の1/1000程度の剛性低下率を考えるね。1/100にしたりすると降伏後の耐力上昇が大きくなりすぎたりするからね。」
|
| 中沢: |
「という事は、基本的にフラットと考えるわけですね。」
|
| 島課長: |
「フラットにするということは、剛性を持たないことになり、するとその部材の塑性率が求められなくなるんだ。だから塑性率を知るために解析上は小さな剛性を持たせるわけだ。図1のS造における第2配についてもフラットでなく同じことがいえるね。」
|
| 中沢: |
「先ほど、終局モーメントMyと言っていましたがMyは降状モーメントではないのですか?」
|
| 島課長: |
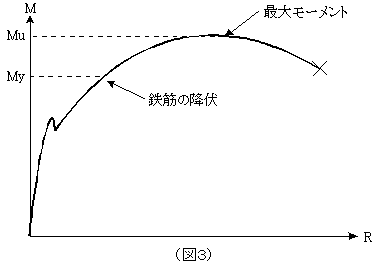
「ちょっと整理してみよう。図3のようにRC造の場合、鉄筋が降状するときのモーメントを降状モーメントMyと呼び、さらに耐力が上昇して最大モーメントに達する。そしてこの点を理論式上では終局モーメントMuと呼ぶわけだ。」
|
| 中沢: |
「ええそうですよね。」 |
| 島課長: |
「この第3勾配の始まる点を、降状モーメントとするか、終局モーメントにするかの判断もあるわけだが・・・。」
|
| 中沢: |
「はい??」 |
| 島課長: |
「すなわち、終局モーメントにすれば第3勾配はフラット(K/1000の勾配)として考えることができ、降状モーメントとすれば例えばK/20の勾配を持たせるなどの考え方となるわけだ。ところが復元力特性の表現上は、どちらの値を採用してもMyと表しているのが多いってわけなんだ。」
|
| 中沢: |
「混乱しそうですが、わかりました。ところで第2勾配は?」
|
| 島課長: |
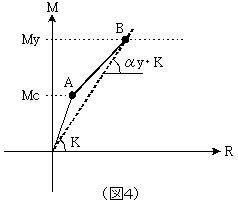
「第2勾配は図4で示すように、弾性剛性(K)に降伏時剛性低下率(αy)を乗じた勾配とMyの交点Bと第1勾配とひび割れモーメント(Mc)の交点Aとを結んだ勾配となるんだ。」
 |
| 中沢: |
「降伏時剛性低下率(αy)は式として与えられているのですか。」
|
| 島課長: |
「そうだね。実験により得られた式がRC規準で示されているね。」
|
| 中沢: |
「部材の曲げ剛性についてわかってきましたが、その他の剛性はどうなりますか?」
|
| 島課長: |
「軸剛性も側柱などでは塑性化するので、弾塑性の扱いだね。せん断剛性については壁は弾塑性で、柱・梁はせん断変形が小さいので弾性剛性でよいと思うね。」
|
| 中沢: |
「なるほど、曲げ、せん断、軸剛性ともそれぞれ決定するわけですね。そこで、どうもわからないことがあります。それぞれの剛性を独立に設定すると言うことは、どういう部材モデルを考えればよいわけですか?」
|
| 島課長: |
「例えば、弾塑性部材モデルとして多用されている材端バネ要素を使うかな。部材モデル図を描くと、図5のようになるね。」
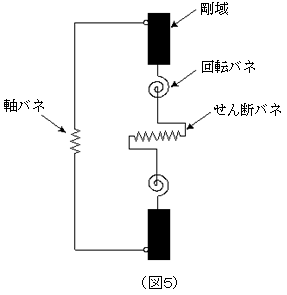 |
| 中沢: |
「なるほど、それぞれ独立に剛性を定義して、それを組み合わせたモデルってわけですね。」
|
| 島課長: |
「さて、さらにひび割れモーメント(Mc)や降伏モーメント(My)は、部材軸力によって値が変動するということも頭にいれてないといけないね。」
|
| 中沢: |
「やはり聞けば聞くほど複雑ですね。ところで、この部材の剛性と串ダンゴ系の振動解析とが、まだ結びつかないのですが。」 |
| 島課長: |
「まずは、この部材の剛性を精度良く求めることが基本だね。この後は2通りの道がある。1つは、この部材レベルの弾塑性剛性をそのまま用いて柱、梁部材で構成する建物全体の振動解析をする方法だ。もう1つは、この部材レベルの弾塑性剛性から、層レベルの弾塑性剛性を導き出し、串ダンゴモデルに置換してから、振動解析する方法だ。前者を精算弾塑性応答解析法と呼び、後者を略算弾塑性応答解析法と呼ぶんだ。」 |
| 中沢: |
「通常はこの略算法が使われているんですよね。」 |
| 島課長: |
「そう。評定*1物件のほとんどは、この略算法が使われているね。物件によっては精算法で検証しながら、最終的には略式法で報告書をまとめ評定取得していることもあるね。精算法は計算時間の点でまだ問題は残っているんだ。略算法は整形な建物ではかなりの精度で、しかも短時間で結果が得られるので良く使われるね。」
|
| 中沢: |
「わかりました。その略算法についてもう少し教えて下さい。」
|
| 島課長: |
「部材レベルの剛性から層レベルの剛性を導くには、保有水平耐力計算と同等な静的弾塑性解析をすることになる。」
|
| 中沢: |
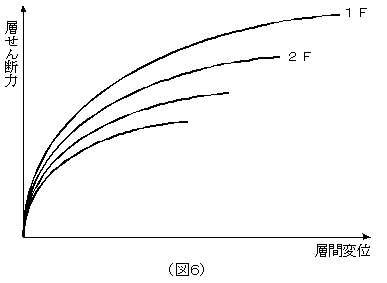
「なるほど、すると層ごとのせん断力と層間変位の関係図が得られますね。これが層レベルの剛性に相当するわけですね。」
|
| 島課長: |
「そういうことになるが、この図6のなめらかな曲線をトリ・リニア型のモデルにしなければならないんだ。」
|
| 中沢: |
「えっ?せっかく精度良い剛性評価のもと曲線の履歴を導き出したのに、さらに簡単な剛性にしてしまうのですか?」
|
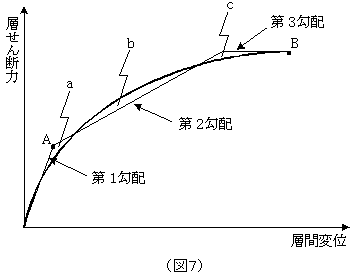
| 島課長: |
「もちろん、適当にモデル化してはいけないんだけどね。図7を見てごらん。層せん断力と層間変位の関係を、トリ・リニア型にモデル化する一つの方法として、エネルギーを等しく保つ方法がある。この場合には、曲線からはみ出した領域(a面積+c面積)と曲線の内側領域b面積が等しくなるように設定しなければいけないんだ。」
|
| 中沢: |
「なんかわかった気がしますが、面積が等しくなるような勾配の組み合わせは、1つ以上あるように思いますね。」
|
| 島課長: |
「そう。そこで第1勾配と第3勾配は曲線との接線勾配を使うことになるね。特に第1勾配と第2勾配の節点Aは、ある部材が最初に塑性ヒンジになった時の層せん断力を採用することなど考えられるが、まぁ、この辺は設計者の判断になるね。」
|
| 中沢: |
「なんとなく解ってきました。」 |
| 島課長: |
「詳しくは学会の地震荷重※2に載っているね。」 |
| 中沢: |
「あとで読んでみます。ところでこの剛性評価は、層に於けるせん断剛性を評価したことになるんですか?」
|
| 島課長: |
「その通りなんだが、もう少し深い話があるんだ。」 |
| 中沢: |
「深い話とは?」 |
| 島課長: |
「建物が高層になると、建物の曲げ変形が生じるんだ。」
|
| 中沢: |
「曲げ変形とは、引張側柱と圧縮側柱の軸変形により生じる建物全体の曲げ型変形ですね。」
|
| 島課長: |
「そう。図7における水平変位には、建物の曲げ変形分が含まれていることになるね。」
|
| 中沢: |
「するとどうなりますか?」 |
| 島課長: |
「この時は、曲げ変形分とせん断変形分に分離しないといけないんだ。」
|
| 中沢: |
「水平変位を分離するんですか?」 |
|
(星 睦廣) |













